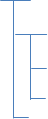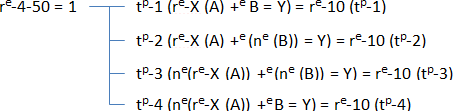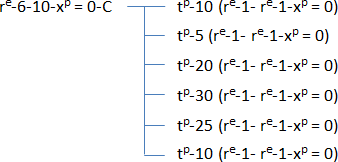
Mathématique circulaire

Partie 1 – Le concept hiérarchique
1.1 Introduction
1.2 La logique de la hiérarchie numérale
1.3 Initiation aux opérateurs (et symboles) de base
1.4 Formules complexes
Partie 2 – L’application
2.1 Les facteurs hiérarchiques
2.2 Fonctions composées
2.3 Opérations multiples
Partie 3 – Coordination
3.1 Le plan cartésien hiérarchique
3.2 Utiliser le plan cartésien hiérarchique
Le contexte de naissance de la mathématique circulaire a débuté lorsque le chercheur s’est penché sur l’élaboration de théories sur l’évolution. Ces théories furent élaborées pour trouver une forme de hiérarchie dans la mathématique plutôt que de promouvoir l’égalité comme dans la mathématique usuelle. Le concept de hiérarchie en mathématique est une inégalité qui permet d’appliquer des changements dynamiques dans la valeur des nombres.
Depuis ces théories sur l’évolution, la mathématique circulaire a été étudiée pour élaborer un logiciel de création graphique, et aussi le chercheur se penche sur la possibilité d’innover dans plusieurs domaines en mathématique, en physique, et en informatique.
Nous verrons à partir de ce document plusieurs ébauches sur la mathématique circulaire entre autres dans l’élaboration de formules nouvelles, de nouveaux opérateurs, et de nouvelles règles en mathématique.
 |
Retour au haut de la page |
Pour créer une hiérarchie, nous devons créer une inégalité, donc l’unité ne doit pas servir à créer les valeurs des nombres. Pour créer la valeur des nombres, nous utilisons un tabloïde qui définit la valeur des nombres hiérarchique de façon à permettre aussi que la valeur de chaque nombre puisse être modifiée en cours d’utilisation dans une formule. Ce qui signifie que le tabloïde sert à initialiser la valeur des nombres avant l’utilisation de la formule.
Deuxième aspect, la hiérarchie des nombres existe que si les nombres sont inégaux par rapport à l’unité. Mais évidemment, même si nous utilisions des valeurs de nombres à virgule, il n’en est pas moins que l’unité devient plus petite et que nous utilisons l’unité en fin de compte. Mais nous ne devons pas utiliser d’unité, même si elle est plus petite. Cela forme une marge d’espacement entre chaque nombre qui est inclus dans la valeur du nombre, mais pas exactement comme vous pouvez le voir actuellement. La valeur devient composée. Une valeur composée n’est pas un indice ou une adresse sur une ligne, c’est une valeur qui est typique au nombre lui-même. Par exemple, pour un nombre hiérarchique, il ne commence pas à 0, mais entre 2 symboles, ou 2 sous-indices.
Pour créer la valeur d’un nombre hiérarchique, par exemple, utiliser « 1.02 » et « 2.64 ». Ces 2 bornes forme une plage, mais ce n’est pas la différence entre les bornes qui forme la valeur, c’est ce qu’il faudrait pour les coller au nombre hiérarchique suivant qui lui aussi a 2 bornes. Les bornes sont là pour créer une impossibilité à coller 2 nombres hiérarchiques ensemble. Donc les bornes, contrairement à une unité, ne donnent pas de valeur unitaire, elles distancent les nombres hiérarchiques de façon inégale. Et la valeur du nombre hiérarchique est comprise entre ces bornes. Pour un autre nombre hiérarchique, les bornes ne doivent pas former une unité qui est comme un autre nombre hiérarchique.
De plus, pour ne pas que les bornes d’un nombre soient joignables avec les bornes d’un autre nombre, nous utilisons une variable « espace » qui définit l’espace occupé par la valeur du nombre. L’espace ne sert pas à redéfinir les bornes, l’espace est ce qui crée une inégalité entre chaque nombre hiérarchique dans leur borne. Puisqu’en réalité l’espace est la variable qui contrôle la convertibilité des bornes pour rendre les valeurs des nombres hiérarchiques inconvertibles.
Voilà la hiérarchie, les valeurs des nombres ne sont pas comparables à ce point-ci, mais n’empêche que l’on peut logiquement savoir quel nombre vaut plus qu’un autre. Vu que les nombres hiérarchiques ne sont pas des indices, ils ont une profondeur, alors il est dit que la profondeur crée les niveaux hiérarchiques.
 |
Retour au haut de la page |
Opérateur « +e » :
L’opérateur « +e » est utilisé pour la concaténation ou la soustraction d’espace dans un nombre hiérarchique. Par exemple, vu que les bornes d’un nombre hiérarchique sont définies indépendamment de la variable « espace » du nombre hiérarchique, cela forme un espace pour chaque unité entre les bornes, donc nous pouvons décider de manipuler l’espace contenu dans la variable espace. Pour ce faire, par exemple, si nous utilisons la formule « 1 +e 1 », cela ne donne pas 2, cela permet de retranché 2 fois de l’espace dans le nombre hiérarchique « 1 ».
Opérateur « = » :
Où va l’espace retranché d’une formule ? Elle peut être affectée à une variable. Par exemple, si nous ajoutons l’opérateur « = », cela signifie que l’on fait une affectation dans une formule. Par exemple, « 1 +e 1 = 2 » signifie que l’on retranche 2 espaces au nombre hiérarchique « 1 » pour les donner au nombre hiérarchique « 2 ».
Symbole « 0 » :
Nous pourrions créer un autre exemple, « 1 +e 0 = 2 » : dans cet exemple, le « 0 » est utilisé non comme nombre hiérarchique, mais comme entité dans une formule symbolisant dans ce cas-ci que l’opérateur « +e » s’applique seulement sur le nombre hiérarchique « 1 » (le premier polynôme de la formule).
Dans la formule « 1 +e 0e = 2 », le « 0e » signifie que l’on affecte au 2 un espace original du nombre hiérarchique « 1 ». Cela a son utilisé lorsque l’on fait des opérations à valeurs répétitives.
Symbole « , » (virgule) :
Si nous écrivons « 1 +e 1 = x,2 », cela signifie que 2 espaces sont affectés à la variable « x » et « 2 ». Le symbole virgule permet de dupliquer une opération sur plusieurs variables. Par exemple, nous pourrions écrire « 1,0e +e 0 = 2 », cela signifie la même chose que « 1 +e 0e = 2 » (vu au paragraphe précédent). Dans le contexte où nous utilisons la virgule dans « 1,0e +e 0 = 2 », nous dupliquons l’application de l’opérateur « +e » sur le second terme (après la virgule). Donc, nous pourrions écrire une série de nombres hiérarchiques « 1,1,1,2,3,4 +e 0 = 2 ».
Opérateur « +i » (concaténation indicielle) :
Comme dans la mathématique ordinaire, l’opérateur « +i » peut être utilisé pour des équivalences, mais ne sert pas seulement à cela en mathématique circulaire. D’abord « +i » fait en même temps le « + » et le « - » selon de la manière qu’il est utilisé. Par exemple, dans la formule « 1 +i 1 », cela signifie que l’on remplace le nombre hiérarchique 1 dans le nombre hiérarchique 1. Donc « 1 +i 1 = 2 » est l’équivalent de « 1 +i 0 = 2 » ou « 1 +i 2 » et signifie en réalité que l’on remplace la valeur du nombre hiérarchique 2 par la valeur du nombre hiérarchique 1.
Pour l’équivalent de « 1 + 1 = 2 » en mathématique ordinaire, donc pour que ça donne 2 fois le nombre 1, nous devons utiliser l’opérateur « +i » de cette façon : « 1,0e +i 0 = 2 ».
Comme dit, nous utilisons aussi l’opérateur « +i » pour faire l’équivalent d’une soustraction. Dans la formule « 1 +i 0 = 2 », cela signifie que nous remplaçons la valeur du nombre hiérarchique « 2 » par le nombre hiérarchique « 1 », donc il y aurait une soustraction si par exemple la valeur du nombre hiérarchique 2 était supérieure à la valeur du nombre hiérarchique 1 avant l’application de la formule.
Opérateur « b+ » :
Cet opérateur sert au contrôle des bornes. Par défaut, seule la borne de référence peut être modifiée dans les formules, donc la borne supérieure, mais nous verrons comment affecter la borne inférieure. Dans une formule, si nous écrivons « 1 b+ 1.0 », cela affecte l’ajout de 1.0 à la borne supérieure du nombre hiérarchique 1. Note : les valeurs affectées aux bornes doivent toujours être des nombres décimaux (séparé par un point pour ne pas être confondu avec le symbole virgule).
Si nous écrivons la formule « 1 b+ 0 = 2 » cela signifie que nous remplaçons les bornes du nombre hiérarchique 2 par les bornes du nombre hiérarchique 1. Si nous écrivons la formule « 1,2 b+ 0 = 3 », cela signifie que nous remplaçons les bornes du nombre hiérarchique 3 par la concaténation des bornes supérieures des nombres hiérarchiques 1 et 2.
Pour affecter la borne inférieure, nous devons utiliser le symbole « 0 » après l’opérateur « = ». Donc, dans la formule « 1 b+ 1.0 = 0 », cela signifie que l’on ajoute 1.0 à la borne inférieure du nombre hiérarchique 1. L’équivalent s’écrit aussi « 1 b+ 1.0 = 1,0 » qui signifie la même chose. Nous pourrions aussi écrire :
« 1 b+ 1.0 = 2,0 » : signifie que nous remplaçons la borne inférieure du nombre hiérarchique 2 par la concaténation de la borne supérieure du nombre hiérarchique 1 et de 1.0;
« 1,0 b+ 1.0 = 2,0 » : signifie que nous remplaçons la borne inférieure du nombre hiérarchique 2 par la concaténation de la borne inférieure du nombre hiérarchique 1 et de 1.0;
« 1,2,3,0 b+ = 2,0 » : signifie que nous remplaçons la borne inférieure du nombre hiérarchique 2 par la concaténation de la borne inférieure des nombres hiérarchiques 1, 2 et 3.
La soustraction de la valeur d’une borne sera expliquée plus loin. Cela est bien différent puisque nous ne souhaitons pas avoir une borne à valeur négative. De plus, il est a noté qu’une affectation d’une plus grande valeur à la borne inférieure que celle de la borne supérieure produit des sens inverses, nous verrons l’utilité plus loin.
Opérateur « re » et symbole « - » :
L’opérateur « re » permet de répéter un espace, et il est attaché au symbole « - » qui sert à attacher une valeur à un opérateur. Par exemple, dans la formule « 1 re-1 = 1 », nous affectons un espace (répété 1 fois) au nombre hiérarchique 1 en provenance du même nombre : cela soustrait de l’espace puisque l’opérateur « +e » ne permettait pas cela implicitement, sauf si nous aurions écrit « 1 +e 0 = 1 », mais cela n’a aucun effet sur l’espace si les bornes forment 1 unité. Note : avec cet opérateur, les bornes sont redéfinies dans la formule « 1 re-1 = 1 », c’est de cette façon que nous pouvons aussi diminuer les bornes. Explicitement, la valeur initiale d’une borne inférieure est fixée au début, mais peut être augmentée ou réinitialisée avec soit la valeur d’une borne d’un autre nombre hiérarchique ou soit sa valeur initiale avec un opérateur que nous verrons plus loin.
Si par la suite nous voulons créer une suite logique comme les nombres de la mathématique ordinaire, alors nous écrivons « 1,0 b+ = 2,0 », « 1 b+ = 2 », et « 1 re-2 = 2 ». Évidemment, nous pourrions aussi créer une suite de nombre ordinaire sans jouer sur l’espace, mais les bornes.
L’opérateur « re » peut aussi être utilisé sans le symbole « - ». Avec la formule « re 0 = 1 », nous supprimons le nombre hiérarchique 1 : avec la mathématique circulaire, nous pouvons supprimer des entités. Avec la formule « re 2 = 1 », nous remplaçons le nombre hiérarchique 1 par le nombre hiérarchique 2. Avec la formule « re 1,2 = 1 », nous effectuons une fusion des nombres hiérarchiques 1 et 2. Avec la formule « 0 re 2 = 1 », nous recréons l’entité 1 en prenant comme base le nombre hiérarchique 2. Avec la formule « 1 re 2 = 3 », nous remplaçons le nombre hiérarchique 3 par le nombre hiérarchique 2 à condition que le nombre hiérarchique 1 soit inclus dans le nombre hiérarchique 2 : la condition sera très utile, nous le verrons un peu plus loin dans le document.
L’opérateur « xp » :
L’opérateur « xp » est l’opérateur d’art de la mathématique circulaire (le x signifie multiple et le p signifie partage). Avec cet opérateur vous pouvez transformer des nombres hiérarchiques en mode multiple utilisation comme pour créer des nombres composés ou créer des fonctions composées.
Dans la formule « 1 xp 1 », l’espace n’est pas retranché, mais il est multiplié. Si vous écrivez « 1 xp 0 = 2 » vous multipliez l’espace pris dans le nombre hiérarchique 1 vers le nombre hiérarchique 2 pour toutes les unités comprises entre les bornes du nombre hiérarchique 2.
Dans la formule « 0 xp 0 = 2 », le nombre hiérarchique existe, mais contient 0 espace dans les unités entre les bornes.
Dans la formule « 1 xp-3 = 0 », cela crée 3 espaces flottants à partir du nombre hiérarchique 1. C’est ainsi que l’on peut avoir de l’espace dans la mathématique circulaire sans avoir de nombre accroché à ces espaces. Nous verrons plus loin la grande utilité de cela.
Dans la formule « xp-3 = 0 », cela crée des espaces nuls qui sont quand même des espaces, mais qui ont une valeur attractive. Ainsi nous pouvons doser l’attraction entre 2 nombres de la manière suivante « xp-1 = 1,2,3 » : cela a pour effet de créer une attraction de 1 espace nul entre les nombres 1 et 2, et entre 2 et 3. Cela forme un nombre hiérarchique composé 123.
Si nous écrivons « 1 xp-4 = 1,2 », cela donne 4 espaces du nombre hiérarchique 1 entre les nombres hiérarchiques 1 et 2. Ce n’est pas l’inverse de l’attraction, c’est seulement qu’ils sont distancés de la sorte et ainsi cela forme un nombre hiérarchique composé 12.
 |
Retour au haut de la page |
Comme cela n’avait pas été expliqué avant, nous allons maintenant aborder le sujet d’ascension du hasard. Dans la mathématique circulaire, il y a un avantage, les résultats sont uniques. Ce qui signifie qu’en physique, nous arrivons à expliquer certains phénomènes grâce à la mathématique circulaire. Mais nous n’aborderons pas tous ce que cela peut engendrer, seulement une partie que nous verrons tout au long de ce document.
Pour qu’il y ait ascension du hasard, à chaque fois que nous utilisons un espace, cet espace est retranché du nombre hiérarchique. Mais le nombre hiérarchique est sans fin et ne s’épuise pas vraiment puisque l’espace restant est toujours partagé entre les bornes, donc l’espace est infini. Cependant, la valeur de l’espace change à chaque utilisation.
Il y a exception : s’il n’a qu’un seul espace entre les bornes, alors l’espace devient nul s’il est utilisé, mais le nombre hiérarchique existe encore. Pour recréer de l’espace, il suffit d’employer la formule « re-2-50 = 1 ». En physique cela s’appelle une application du concept de l’espace recrée qui est un concept expliqué dans le document « Les clés de la physique ». Dans cette formule, nous créons la répétition de 2 unités de 50 espaces dans le nombre hiérarchique 1.
Pour débuter avec des formules complexes, nous allons aborder ce qui s’appelle l’espace composé. L’espace composé est la façon dont nous allons obtenir des résultats concrets avec la mathématique circulaire. Tout d’abord, débutons avec la formule suivante :
Dans cette formule nous utilisons le symbole « - ». Ce symbole est pour l’implémentation d’une première branche d’une hiérarchie. La formule ne présente que des hiérarchies simples. L’explication de cette formule est la suivante : « xp-3 = 0 » crée trois espaces flottants, « re-2 » crée 2 répétitions, et « -1 » signifie d’ajouter ces 2 répétitions de 3 espaces flottants au nombre hiérarchique 1. Ce qui signifie que l’espace est composé dans ce nombre hiérarchique de 3 divisions par unité dans une dimension flottante. Donc nous pouvons ensuite utiliser le symbole de hiérarchie à 3 branches pour toute manipulation de ce nombre hiérarchique :
Dans cette nouvelle formule, nous retranchons 1 espace au 2e niveau hiérarchique du nombre hiérarchique 1 pour le déplacer vers le nombre hiérarchique 2. Évidemment, vu que l’espace est flottant, alors il conserve sa position hiérarchique (2e) initiale du nombre 1 lorsqu’il est placé dans le nombre 2.
Le rôle de l’espace flottant est de différer la valeur de l’espace premier. Cette différenciation vient ajouter à l’espace premier une multiplication de l’espace dans une dimension qui peut être multiple. Nous pouvons utiliser plusieurs valeurs dans un seul nombre hiérarchique, ce qui le rend explorable. L’exploration est la clé même de la mathématique circulaire. Dans l’univers, l’espace joue le rôle de rendre explorable l’environnement physique des choses. L’exploration à l’intérieur d’un nombre lui permet d’avoir une profondeur, donc de pouvoir contenir quelque chose plutôt que d’être un simple indice comme les nombres de la mathématique ordinaire. Ici, le nombre est plus qu’un symbole servant à calculer, c’est une source de valeurs. Penchons-nous sur l’étude de cette source de valeurs.
L’opérateur « = » peut être placé devant le nombre hiérarchique ayant plusieurs niveaux hiérarchiques :
Cette nouvelle formule crée ce qu’on peut appeler l’amplitude hiérarchique. Dans ce contexte, la hiérarchie se développe à l’intérieur même du 2e niveau hiérarchique des nombres hiérarchiques 1 et 2.
Nous pouvons observer à présent qu’il existe bel et bien la possibilité de créer des nombres hiérarchiques à partir de simple formule en mathématique circulaire.
 |
Retour au haut de la page |
Nous avons vu que la variable espace existait, en réalité ce n’est pas le seul élément, il y a d’autres facteurs hiérarchiques. Les mathématiques circulaires sont vraiment bien pensées pour créer des modèles en physique. Tout d’abord, nous avons observé précédemment le comportement des opérateurs sur l’espace. Ce sont les mêmes opérateurs qui doivent être utilisés pour d’autres éléments qui sont eux aussi des facteurs hiérarchiques.
L’autre facteur que nous allons aborder a été baptisé « hiérarchie inverse ». Ce facteur est composé d’une mémoire, donc nous allons aborder la gestion de la mémoire avec la mathématique circulaire.
La hiérarchie nous permet d’enregistrer de l’espace à l’intérieur de bornes. Donc, nous allons nous servir du même genre de principe sauf pour créer des positions hiérarchiques dans ce qu’on peut appeler un plan cartésien hiérarchique.
Dans la hiérarchie simple (ou traditionnelle) présentée à la figure 1, nous comprenons ce diagramme hiérarchique. Une mémoire pourrait être créée en fonction de la position développée. Ce genre de mémoire est celle que l’on retrouve généralement dans tous les systèmes utilisant la mathématique ordinaire. Mais maintenant, vous verrez à la figure 2 que le diagramme hiérarchique peut être développé selon la position de la sous-branche et non de la branche supérieure.
Dans le nombre hiérarchique, nous pouvons définir les bornes et aussi décaler les espaces contenus dans ces bornes. Ce qui signifie que cela permet de définir une mémoire en utilisant toutes les positions hiérarchiques, donc il n’y a plus d’exclusivité. Nous obtenons alors une mémoire issue du concept de la hiérarchie inverse.
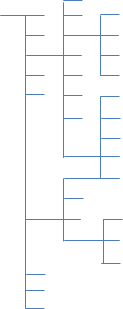
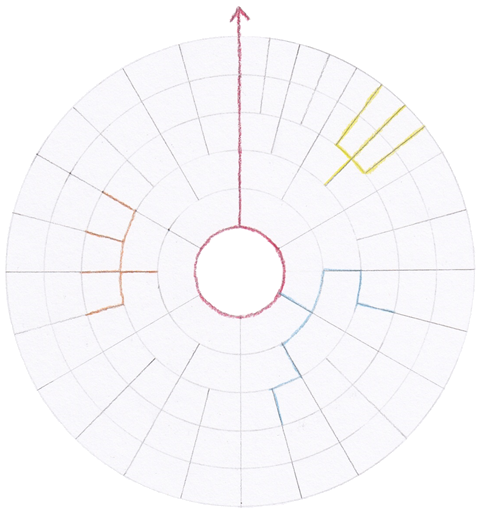
La figure 2 présente un diagramme de la hiérarchie inverse. Il faut constater qu’il y a une branche qui embarque sur une autre branche, c’est la principale raison pourquoi nous l’appelons la hiérarchie inverse. D’abord, cela ne mêle pas au niveau de la mathématique puisqu’en fait, les branches de niveau hiérarchique plus élevé ne se touchent pas. Cela sert à créer un point « O » (cercle) dans la hiérarchie. Nous verrons l’utilité des points « O » plus loin.
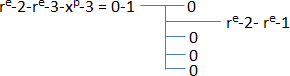
La formule suivante sert à créer le premier niveau hiérarchique inverse :
Cette formule servait à créer le diagramme hiérarchique suivant :
Cette formule s’explique de la façon suivante : avec le terme « xp-3 = 0 » nous créons trois espaces flottant à l’intérieur du terme « re-2-re-3 » (qui signifie la création de répétition de 2 sections, une de 2 répétitions et l’autre de 3), tout ça affecté à la variable hiérarchique 1 (après le « = », il y a « -1 »). Si nous avions écrit « re-2-re-3-re-1-xp-3-xp-4 = 0-1 » sur le premier terme de la formule, nous aurions obtenu le diagramme hiérarchique inverse suivant (au 1er niveau) :
La hiérarchie inverse peut se mêler aussi à l’espace, comme par exemple dans la formule « re-2-50-re-3-xp-3 = 0-1 », le terme « re-2-50 » permet de créer de 2 unités de 50 espaces. Il est aussi possible de personnaliser chaque unité avec un terme « re-2-50-25 ». Il est a noté que l’espace omise dans la formule entraîne que nous utilisons la dernière personnalisation de l’espace pour créer sa valeur, donc « re-4-50-25-75 » fera en sorte que les 2 dernières unités soient à 75 espaces.
Nous allons voir maintenant comment créer un point « O » (cercle) dans le diagramme de la hiérarchie inverse. Pour y arriver, nous devons aborder le 3e facteur. Précédemment, nous avons abordé les facteurs « espace » et « mémoire » (hiérarchie inverse). Le 3e facteur est le temps.
Le temps est à l’origine une synchronisation mécanique avec la mathématique ordinaire. Cependant, le facteur temps avec la mathématique circulaire s’appellera aussi « temps inverse ». Le temps inverse est en quelque sorte pour signifier le passé, le présent et le futur : donc, c’est la ligne de temps. Mais le temps inverse permet aussi de déterminer des distorsions dans le temps, puis pour rattraper le temps ayant une distorsion. Mais plus spécifiquement, nous ne jouons pas à créer des distorsions dans le temps, ces distorsions se créent toutes seules avec la mathématique circulaire et son facteur temps.
Un nouvel opérateur est utilisé pour le temps, l’opérateur « tp » : l’abréviation « t » signifie « temps » et « p » signifie « partage ». L’opérateur s’utilise comme tel « tp-50 = 1-re-0 ». Dans cette formule « 1 » est le nombre hiérarchique 1 qui se fait affecté à la suite de l’opérateur « = », « -re-0 » signifie pour toutes les unités du nombre hiérarchique 1, et « tp-50 » signifie que l’on affecte 50 temps par unité au nombre hiérarchique 1. Si nous avions écrit « tp-50 = 1-re-2 », cela signifie que nous affectons les 50 temps aux 2 premières unités du nombre hiérarchique 1. Si nous avions écrit « tp-50-25 = 1-re-2-re-3 », cela signifie que nous affectons 50 temps aux 2 premières unités et 25 temps aux 3 dernières.
Les lignes de temps se lisent toujours en temps pareil dans un diagramme hiérarchique d’un nombre. Donc s’il est défini 50 temps à plusieurs endroits, ils sont dans le même temps, etc. Un temps ayant moins que l’autre signifie que c’est le passé de l’autre. Le même temps est aussi une façon d’appeler cela le point « O » (cercle) que nous avons mentionné précédemment. Il est possible de définir des temps uniques systématiquement si on le désire. Par exemple si nous plaçons le nombre hiérarchique devant « tp » de cette façon « 1 tp 0 = 2-re-0 ». Cette dernière formule signifie que le temps de la première unité (par défaut) sera retranché comme l’espace à chaque fois que l’on affecte une unité dans le nombre hiérarchique 2. Puisque le temps est uni (point « O ») par le même nombre, toutes les unités du point « O » se font réajuster en fonction du temps restant lorsqu’une unité de temps est retranchée. Il se peut que des points « O » se fusionnent s’ils sont du même nombre lorsque les opérations de retranchement de temps sont effectuées.
La lecture du temps sert aussi à rejoindre les unités. Avec le point « O », nous pouvons rejoindre plusieurs unités en même temps. Les opérations sur le temps s’effectuent de la manière suivante. Avec la formule « re-1-100 = 1 tp-50 », cela signifie que toutes les unités ayant 50 temps dans le nombre hiérarchique 1 se voient remplacer leur espace par 100. Avec la formule « re-2 = 1 tp-50 », cela signifie que toutes les unités ayant 50 temps dans le nombre hiérarchique 1 se voient ajouter une unité supplémentaire, donc doublement d’unités qui gardent les mêmes paramètres.
D’autres opérations peuvent être effectuées avec le temps comme l’affectation d’une nouvelle valeur à une borne : formule « b+-1.25 = 1 tp-50 », qui affecte la valeur 1.25 à la valeur actuelle de la borne supérieure de toutes les branches hiérarchiques ayant au moins un temps de 50. Pour l’affectation d’une borne inférieure, cela se fait avec la formule « b+-1.25 = 1,0 tp-50 » : nous avons ajouté « ,0 ».
Pour faire diverses opérations possibles, n’oubliez pas que vous pouvez utiliser « 0 exposant » qui signifie « à valeur originale » dans la plupart des cas, comme dans la formule « 1 tp 0t = 2-re-0 » . Mais nous pouvons aussi utiliser pour les bornes, comme dans la formule « b+-0.1 = 1,0b tp-50 » qui signifie de conserver la valeur de la borne inférieure originale du nombre hiérarchique 1, mais de décalé de 1 unité toutes les autres unités, ce qui permet l’ajout d’unité en début de branche hiérarchique, ce que nous ne pouvions pas faire avec « re-2 = 1 tp-50 ».
 |
Retour au haut de la page |
Pour comprendre et percevoir l’utilité de la mathématique circulaire, il faut apprendre à créer des fonctions composées. Une fonction composée permet de faire le lien entre la théorie et la pratique. Commençons dès maintenant à voir comment nous pouvons faire des fonctions composées et voir leur application ensuite dans la réalité.
Pour créer des fonctions composées, nous utiliserons en général les mêmes opérateurs que ceux vus précédemment, sauf qu’ils seront utilisés dans un contexte de fonction, donc pour permettre des imbrications d’instructions.
Vu que nous avons utilisé l’espace sous forme de variable, alors cette variable sera contenue entre parenthèses « ( » et « ) », et pourra contenir des formules et des instructions, cela désigne l’espace. Le diagramme hiérarchique sera toujours utilisé pour les fonctions composées, et le temps sera aussi une référence sur une partie d’une fonction. De plus, le temps pourra être muté à des variables.
Fonction composée :
1 (tp-50) +e 2 (tp-100) = 3
Dans cette fonction, cela signifie que nous mutons toutes les unités de temps 50 contenues dans le nombre hiérarchique 1 avec toutes les unités de temps 100 contenu dans le nombre hiérarchique 2, pour les affecter ensuite au nombre hiérarchique 3.
Fonction composée :
re-2 (1 tp-50) = 2
Dans cette fonction, nous récupérons 2 unités de temps 50 contenues dans le nombre hiérarchique 1 pour les affecter dans le nombre hiérarchique 2.
Fonction composée :
re-2 (1 (0e)) = 2
Dans cette fonction, nous répétons 2 fois le contenu de la parenthèse (espace) qui elle-même contient l’extraction d’un espace à valeur originale du nombre hiérarchique 1, et cet espace multiplié 2 fois est ensuite affecté au nombre hiérarchique 2.
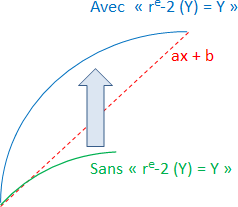
Fonction composée :
re-X (A)) +e B = Y
Cette fonction est l’équivalent de la fonction mathématique ordinaire y=ax+b. Les variables s’écrivent toujours en lettre majuscule pour ne pas être confondues avec les opérateurs. Une variable est l’équivalent d’un espace. Nous pourrions remplacer ces variables par d’autres formules de la mathématique circulaire.
Fonction composée :
tp-1 (re-2-30-40-tp-2-3 = 1) = re-2 (tp-1) = 2
Cette fonction s’explique comme suit : le terme « (re-2-30-40-tp-2-3 = 1) » signifie que nous affectons le nombre hiérarchique 1 de 2 unités ayant un espace de 30 et 40, avec comme temps 2 et 3; le terme « tp-1 (…) » signifie que nous gardons une référence en temps 1; le terme « = re-2 (tp-1) » signifie que nous répétons 2 fois la référence sur le temps 1; et le dernier terme « = 2 » signifie que nous affectons les 2 répétitions de la référence sur le temps 1 à la variable hiérarchique 2.
L’opérateur « fx » (fracturer, casser) :
Ce nouvel opérateur « fx » permet de briser des termes de fonctions, donc briser de l’espace en quelque sorte. Il s’utilise de la façon suivante : dans la formule « (1 tp-50) fx-2 », cela signifie que le temps 50 dans le nombre hiérarchique 1 est fracturé en 2 unités avec leur espace fracturé aussi en 2, mais ils conservent le temps 50. Note : le temps ne se fracture jamais.
 |
Retour au haut de la page |
Vu que nous avons le facteur temps, nous pouvons synchroniser des fonctions à l’intérieur d’un diagramme hiérarchique. Voici une fonction qui synchronise plusieurs formules.
Dans cette formule, le nouvel opérateur « ne » signifie « négation », il transforme une opération en retrait, l’équivalent pour créer des valeurs négatives, sauf qu’il s’applique seulement sur le facteur espace. Par exemple, lorsqu’il transforme un espace en retrait et qu’il reste seulement une unité dans le nombre hiérarchique, alors la borne inférieure obtient une valeur au-dessus de la borne supérieure. Donc, une valeur négative peut être dans le diagramme hiérarchique que si seulement la borne inférieure est en supériorité sur la borne supérieure : donc de l’espace à sens inverse.
Dans la précédente fonction, vu qu’il y a les variables A, X et B, alors la formule attend que l’on comble les valeurs d’origine de ces variables. La fonction exécute une forme de losange, bien qu’à ce stade-ci nous n’avons pas encore vu les formes géométriques, il s’agit ici d’une forme géométrique simple dans ce contexte.
Lorsque l’on fait appel à la précédente formule, nous devons le faire de cette façon : « 1 (1.0 = A-0e, 0.0 = X-0e +e 1.0, 0.0 = B-0e) ». Dans cette formule, nous appelons le nombre hiérarchique 1 qui contient les multiples fonctions, et nous lui demandons d’affecté à la variable « A » la valeur « 1.0 » et ainsi de suite pour les autres variables, ensuite nous spécifions pour la variable X que ça valeur doit être augmenté de « 1.0 » à chaque fois qu’il est appelé (sauf pour la première fois dont la valeur initiale s’exécute). « 0e » symbolise que les variables conservent leur valeur originelle à chaque fois qu’elles sont appelées.
De plus, la mathématique circulaire a l’avantage d’utiliser une même fonction pour créer plusieurs résultats possibles. Dans le dernier cas, nous avions créé un losange, sauf que nous pouvons aussi créer un cercle ou une spirale. Par exemple, si nous appelons le nombre hiérarchique 1 avec la formule suivante « 1 (1.0 = A, 0.0 = X-0e +e 1.0, 0.0 = B-0e, re-2 (Y) = Y) ». Dans ce nouvel appel au nombre hiérarchique 1, nous avons supprimé « 0e » pour l’affectation de la variable A (ce qui cause un retranchement de l’espace, supposons ici que nous avons initialisé cette variable avec au moins 2 unités), et nous avons ajouté une affectation Y de son double, ce qui crée un cercle. Dans ce contexte, ce cercle n’est pas encore parfait puisqu’il faudrait jouer avec certain paramètre comme la durée de la fonction qui est défini à « 10 » dans ce contexte, mais le « 10 » pourrait être remplacé par une variable ce qui nous donnerait une autre marge de manœuvre avec la fonction. Nous traiterons plus loin les fonctions graphiques.
 |
Retour au haut de la page |
À l’origine, le plan cartésien vient de la fabrication de carte. Dans un contexte plus évolué, nous pouvons savoir par exemple que la terre n’est pas plate, ce qui modifie le plan d’une carte. Pour obtenir des précisions impeccables, nous avons besoin d’une version plus évoluée de ce plan cartésien. Quelque chose à la fois qui peut aussi cartographier l’univers.
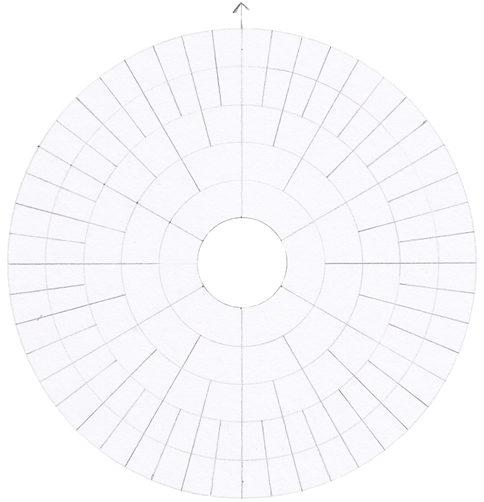
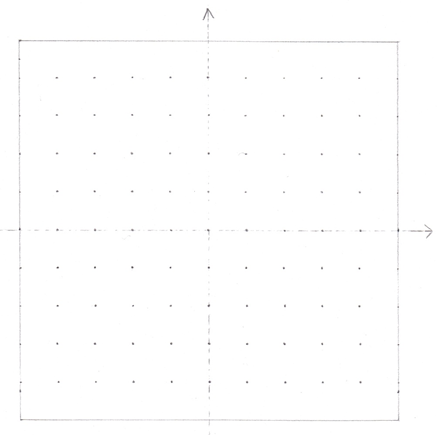
À la figure 3, ce plan cartésien hiérarchique est coloré à certains endroits pour vous montrer l’allure de ce plan cartésien. D’abord, il y a un seul axe (partie colorée en rouge). Le centre n’est jamais utilisé dans le plan cartésien hiérarchique pour la simple raison que le centre n’est pas le point vide du graphique, le centre est le cercle et il y a plusieurs centres. Les parties colorées en jaune, bleu et orange sont des diagrammes hiérarchiques qui peuvent se former à l’intérieur du plan cartésien hiérarchique : c’est aussi la façon dont nous allons utiliser le plan cartésien hiérarchique.
Comme observé, ce plan cartésien n’a pas effectivement la même utilité qu’un plan cartésien ancien. D’abord, l’axe peut aussi fléchir dans un contexte de 3 dimensions. Contrairement au plan cartésien ancien, l’axe peut prendre l’allure d’une courbe, verticale ou horizontale. Ce plan cartésien hiérarchique est conçu pour les mathématiques circulaires, et ne peut pas être utilisé autrement que par la mathématique circulaire.
Le plan cartésien hiérarchique a plusieurs avantages par rapport à l’ancien plan cartésien. D’abord le contexte d’espace ici n’est pas déterminé selon la position d’un point dans le graphique, l’espace est typiquement gérable que par les nombres et variables hiérarchiques. Ce qui permet de déterminer selon un nombre hiérarchique sa quantité d’espace/volume utilisé. Mais, voici l’avantage ultime de ce plan cartésien, c’est qu’il permet de réutiliser un même espace puisque l’espace est accessible selon différents points dans le graphique, donc le plan cartésien hiérarchique permet d’utiliser l’espace selon le concept de l’espace recréé. L’espace recréé est comme nous l’avons défini dans le document « Les Clés de la physique ». Tels nous pouvons maintenant avoir des formes avec des surfaces d’espace recréé, c’est une innovation en mathématique.
Voici comment nous utilisons le plan cartésien hiérarchique. Tout d’abord, nous naviguons dans l’axe principal (partie colorée rouge à la figure 3) avec le temps. Comme le temps ne peut jamais égaler 0, alors le temps 1er est le premier cercle vers le centre du graphique, et les autres cercles sont d’autres temps. Puisque le temps n’égal pas 0, sinon à 0 il n’y a pas de temps, alors l’intérieur du premier cercle au centre n’est pas utilisé.
De plus, le temps est aussi utilisé pour rassembler plusieurs branches hiérarchiques, ce qui constitue un autre développement du concept de l’espace recréé. Tel le temps au point « O » dans un nombre hiérarchique est représenté sur le graphique selon les cercles, donc pas en fonction de position cartésienne ordinaire. Les différents axes dans le graphique peuvent être rejoints à partir du premier axe (partie colorée rouge) par rapport à un autre nombre hiérarchique. C’est ce qu’on appellera « le temps qui se contient ». Telle dans cette définition, les objets (ou nombres hiérarchiques) sont positionnés selon leur temps qu’il contienne entre eux. Donc, un objet s’il est placé seul, commence toujours à exister sur l’axe principal.
Pour contrôler, l’axe que nous utiliserons, nous utilisons évidement les nombres hiérarchiques. Dans un même nombre hiérarchique, sa structure modifie la structure de temps du plan cartésien hiérarchique. Ce qui signifie que sur le plan cartésien hiérarchique, l’ordre est donné selon les nombres hiérarchiques utilisés et non selon la logique dans le graphique comme une suite de nombre logique. Donc, il n’y a pas réellement de suite logique de nombre. La logique n’est pas dans la suite, elle est dans l’interprétation des nombres hiérarchiques.
Tel par exemple, à la figure 4, nous représentons un nombre hiérarchique par la branche principale en premier lieu, le temps « tp » de la première unité. Il est a noté que la première position dépendra du graphique du plan cartésien et le temps. Selon le graphique, en commençant par la première unité nous calculons à partir de cette première unité. Donc, sur le premier cercle du graphique, il y a 6 temps, sur le second, il y a 12 autres temps, et ainsi de suite, donc la position « 50 », par exemple, devrait se trouver sur le 4e cercle. Mais cette position n’est que la position par défaut. Évidemment, nous pouvons jouer avec la définition des temps à l’intérieur du plan cartésien hiérarchique.
Pour modifier et gérer les temps des positions hiérarchiques du plan cartésien, nous utilisons en fait un nombre hiérarchique pour gérer le plan cartésien.
Dans la formule ci-dessus, nous configurons le premier niveau hiérarchique de la variable C (choisi pour « Cartésien »). « xp » est seul pour laisser libre le nombre de niveaux hiérarchiques qui seront créés. Nous pouvons constater que le phénomène d’espace recréé peut s’effectuer même à la définition du plan cartésien. Par exemple, si nous définissons avec « re » au 2e niveau hiérarchique plus de 2 répétitions à certains endroits, alors nous fabriquons un plan cartésien hiérarchique qui n’est pas égal partout comme à la figure 4.
De plus, lorsque le temps est défini, alors le temps par défaut n’est plus le même qu’initialement. Ce qui fait que le temps d’une branche hiérarchique inférieur dépend donc de l’entité supérieure. Dans la formule ci-haut, vu que « tp-10 » est défini, cela engendre que les branches de niveau inférieur commenceront à « tp-11 » par défaut. Le graphique cartésien peut avoir plusieurs fois le même temps à plusieurs endroits, ce qui crée des points « O » (cercle). Donc, pour comprendre, un cercle est un temps dans le graphique, ce qui permet aussi d’unir plusieurs points à la fois. Selon, comment les temps seront définis dans le graphique, alors même si les cercles se suivent physiquement, le temps n’aura pas le même ordre.
Pour poursuivre dans des formules, un peu plus complexes, voici une formule qui positionne le nombre hiérarchique 1 dans la variable C (« C » pour « Cartésien ») :
Dans cette formule, il faut noter que dès que « C » est défini, nous n’avons pas besoin de le redéfinir, « 1 » est seul en supposant qu’elle est déjà définie. Lorsque 1 est placé à cet endroit, il remplace toutes les anciennes dispositions du graphique à cette branche hiérarchique. Pour éviter cela, ajoutez « -0 » après le 1, et le plan cartésien se conserve en y ayant inséré le nombre hiérarchique 1. Le nombre hiérarchique 1 se trouve alors dans une autre dimension du plan cartésien. Nous savons désormais comment créer des dimensions au plan cartésien. Souvenons-nous qu’une variable ou un nombre hiérarchique est une porte d’entrée vers une nouvelle dimension s’il y a « -0 » devant.
Nous avons pu constater une des merveilles de la mathématique circulaire, c’est que les nombres peuvent être insérés dans d’autres nombres. Pour mettre plusieurs nombres dans la même branche hiérarchique, utilisez le symbole « , » comme cela « 1-0, 2-0 ». Les variables ou nombres hiérarchiques peuvent être insérés à plus d’un endroit dans un plan cartésien ou à l’intérieur d’un même nombre ou d’une même variable. Pour les retirer, utiliser « ne (1-0,2-0) ». Nous pouvons détruire aussi une branche hiérarchique avec « ne (0) » appliquer sur la branche que l’on veut supprimer. Maintenant, vous avez appris à gérer un plan cartésien hiérarchique (via une variable hiérarchique).
 |
Retour au haut de la page |
Le plan cartésien hiérarchique s’utilise à l’intérieur d’autres formes de plan cartésien de la mathématique ordinaire. Le plan cartésien hiérarchique est un point sur les autres graphiques cartésiens. On dit que tout est relié dans l’univers, et bien avec une combinaison de la mathématique ordinaire et la mathématique hiérarchique nous arrivons à tous relier ensemble.
Le concept d’utiliser le plan cartésien hiérarchique sous forme de point est enrichissant. D’abord, nous pouvons créer des résultats complexes avec la mathématique circulaire, ce qui permet d’enrichir la tâche de la mathématique ordinaire. Donc, voici ce que peut faire une combinaison des 2 mathématiques.
D’abord, un point est réalisable avec le plan cartésien hiérarchique puisque les bouts se joignent à l’intérieur du concept du graphique à cause du concept de l’espace recréé. Ce qui permet de dire que l’on fait graphiquement des structures circulaires. De plus, il y a le concept 3D qui permet de définir plusieurs dimensions en fusionnant plusieurs plans cartésiens à l’aide de la gestion des variables hiérarchiques. Cela donne naissance à des structures multidimensionnelles que nous appellerons « structures sphériques » qui sont réalisables seulement avec la mathématique circulaire. En quelque sorte, nous appelons ces structures sphériques comme on appelle un point.
Les plans cartésiens matriciels comme ceux utilisés en mathématique ordinaire servent à créer des structures divisibles s’ils sont utilisés seul. L’avantage de l’utiliser avec la mathématique circulaire sera de donner un caractère constructif aux modèles mathématiques. Une structure unie a beaucoup plus d’avantages tant au niveau conceptualisation de forme géométrique ou autres conceptions. Les avantages vous seront présentés au fur et à mesure.
D’abord si nous avons une structure indivisible, tel un point cartésien hiérarchique, ce point permet de résoudre les problèmes au niveau des limites des modèles mathématiques, puisque ce point est comme on peut dire, un objet, et non seulement un indice. L’indice est vide, tandis que le point est plein. Alors nous utiliserons quand même sous la même forme le plan cartésien ordinaire, mais cette fois avec des points au lieu des segments. Dans un certain sens, les graphiques cartésiens à structures sphériques sont à la résolution graphique « dot atomique » qui symbolise « point atomique », représentant une structure finie avec des points.
Sur un plan cartésien sans la mathématique circulaire, les points n’existent pas réellement puisqu’ils sont une partie divisible en 2 ou en plusieurs. Donc, c’est maintenant que l’on doit utiliser la mathématique circulaire pour faire d’un point, un véritable point. Un point est une entité qui peut désormais stocker des informations, des formules et bien plus encore, des structures, etc. Nous ne travaillons pas sur une échelle de volumes seulement.
Avec le plan cartésien « dot atomique », le point peut lui-même se déplacer. Effectivement, cela est possible. Supposons que dans un appel au point P1 (variable hiérarchique), nous écrivons ceci « P1 (Y = P1-Y = P1-Y +e 1.0 = P1-Y) » : dans cette formule nous faisons une affectation de Y (appelé) à P1-Y (qui la position du point P1 sur l’axe des Y), et une affectation encore à P1-Y avec un double déplacement de 1.0.
Un point, plan cartésien hiérarchique, peut contenir plusieurs fonctions, et ainsi renfermer plusieurs courbes sur un graphique cartésien « dot atomique ». Ainsi, lorsqu’un point se déplace, il déplace aussi jusqu’à plusieurs courbes sur un plan cartésien « dot atomique ». Un point est aussi relié à un autre point avec le terme « P1-P2 » qui lie simultanément 2 points ensemble, P1 à P2. Nous pouvons aussi déplacer plusieurs points simultanément avec l’appel à la fonction suivante « P1 (+e P2, +e P3, +e P4, Y = P1-Y +e P2-Y +e P3-Y +e P4-Y) », cela affecte le résultat de Y pour toutes les variables P1 à P4 contenant Y. Nous avons ajouté « +e P… » au début de l’ouverture de la parenthèse, cela est pour ne pas que ce soit interprété comme des variables indépendantes. C’est aussi la méthode pour lier plusieurs points ensemble de façon permanente. Si l’on veut briser le lien, il suffit d’écrire la formule « P1 (ne (+e P2)) ».
Le comportement des points d’un graphique cartésien « dot atomique » demeure indépendant entre eux, même s’ils sont liés.
La fusion des points est un autre élément dont nous allons nous servir. La fusion est un élément qui sert à créer des surfaces, par exemple, pouvant être pleine ou ayant des parties transparentes. Cela peut aussi servir à créer des formes dans la forme.
La fusion commence ainsi par l’absorption de points. Par exemple, l’absorption de points est effectuée par la formule suivante « P1 +e 0-(4.0 = X, 2.0 = Y) +e 0-(5.0 = X, 2.0 = Y) = P1 ». Dans cette formule, le point défini P1 est fusionné avec deux autres points. Les symboles « 0 » et « - » sont utilisés pour symboliser un point flottant sur le plan cartésien « dot atomique ». À l’intérieur de la variable P1, l’accès aux 3 points qu’il inclue se fait simultanément. Ainsi nous pourrions aussi de cette façon créer de la largeur dans une fonction. Cependant, pour que ces points puissent se déplacer en même temps que P1 advenant un déplacement du point, cela doit être indiqué de la façon suivante « P1 (+e 0-(4.0 = X, 2.0 = Y), …) ». Pour supprimer un point fusionné « P1 (ne (+e 0-(4.0 = X, 2.0 = Y))) ».
Il est intéressant de constater qu’un point peut contenir plusieurs points du graphique cartésien « dot atomique ». Cela permet aussi de créer des graphiques cartésiens ayant une forme à la place du point. Pour que cela se fasse, utilisons la formule suivante « P1 = *0 ». Le symbole « * » symbolise « en tout point de ». Pour créer une ligne de points spéciaux « P1 = *0-(2.0 = Y) ». Et appliquer sur une formule du genre y=ax+b : « P1 = *0-(+e 0-(*0 = X, *0 = Y), 0.0 = Y, 0.0 = X +e 1.0 = X, 1.0 = A, 0.0 = B, re-10 (re-A (X) +e B = Y)) », cela dit que les variables X et Y s’initialise à 0.0, pour chaque appel de X, X est augmenté de 1.0, et la fonction est répété 10 fois. Il est à noter que nous avons aussi inclus « +e 0-(*0 = X, *0 = Y) » pour que tous les points fusionner à P1 se déplacent aussi. Si cela avait été omis, la fonction aurait gardé la référence sur les mêmes points fusionnés à P1.
Nous pouvons aussi imprimer en mosaïque une forme fusionnée par ses points. Par exemple, la formule suivante le fait « P1 = *0-(+e 0-(*0 = X, *0 = Y), 0.0 = Y, 0.0 = X, re = *0) » à partir de l’ordonnée à l’origine du graphique cartésien « dot atomique ». Pour une mosaïque avec décalage « P1 = *0-(+e 0-(*0 = X, *0 = Y), 0.0 = Y, 0.0 = X + 0.5 = X, re = *0) ». C’est ainsi que nous pouvons créer toute sorte de matrices de points sur un graphique cartésien « dot atomique ».
De plus, il est important de considérer que nous pouvons relier tout l’univers de point d’un graphique cartésien « dot atomique » en ayant omis « +e 0-(*0 = X, *0 = Y) ».
 |
Retour au haut de la page |
0 commentaire.